【感染症の数理モデル】SIRモデルとは 分かりやすく説明します【シミュレーションあり】

感染症の数理モデルにおける基本であるSIRモデルについて、理解したいと考えている方へ。

この記事では、SIRモデルについて、どのサイトよりも分かりやすく解説していきます。

SIRモデルの特徴

• 感染初期は、指数関数的に感染者数が増加する
• 基本再生産数が1未満であれば、流行しない
• 基本再生産数が高いほど、かからない人は指数関数的に減少する
• 基本再生産数が低いほど、流行のピークが小さくかつピークを迎えるまでに時間を要する

これらをこの記事を読むことによって、理解することができます。

実際に、大学で数学を学んでいる経験をもとに、できる限り分かりやすく説明していきます。

SIRモデルとは 分かりやすく説明します

SIRモデルの定義

仮定

• 全ての人がS,I,Rのいずれかに分類される
• 感染症以外による人口の増減が起こらない
• 一度感染すると、免疫を獲得して、二度とかからない

微分方程式

$$\begin{eqnarray}\frac{dS(t)}{dt} &=& -\beta S(t)I(t) \\ \frac{dI(t)}{dt} &=& \beta S(t)I(t) -\gamma I(t) \\ \frac{dR(t)}{dt} &=& \gamma I(t)\end{eqnarray}$$

\(S(t)\):感受性人口（感染する可能性のある人口）susceptibles

\(I(t)\):感染人口（感染している、かつ感染させる能力のある人口） infected/infections

\(R(t)\):隔離人口（病気から回復による免疫保持者、もしくは隔離者・死亡者）recovered/removed

\(\beta\): 伝達係数 \((\beta > 0)\)

\(\beta^{'}\): 感染率 \((\beta^{'} > 0,\beta = \frac{\beta^{'}}{N})\) ※\(N\)は、全人口とする

\(\gamma\): 回復率・隔離率 \((\gamma > 0)\)、感染期間 = \(\frac{1}{\gamma})\)

\(t\):時間

SIRモデルの考え方

SIRモデルというのは、ある町の中の一人一人がSIRの3つの状態うち、どれか一つに必ず属すことを前提とした、感染症の数理モデルです。図１にSIRモデルの基本的な考え方をまとめました。

3つの状態に分けている人口の増減がこのSIRモデルを用いると、時間変化とともに分かるようになります。

Sは感染する可能性のある人口（実質的に健康でかかったことのない人）、Iは感染している人口（厳密には、感染させる能力がある人のみ対象）、Rは隔離されていてこれ以上感染させることのない人や感染症によって死亡した人や免疫を獲得して二度とかからない人を含めます。

伝達係数βは、感染人口S(t)の減少に比例して低下する

伝達係数は、感染率を全人口で割った値です。なぜ、割るのかというと、微分方程式の一つ目の式を見れば分かる通り、\(\frac{S(t)}{N}\)となり、それに対して、\(\beta^{'}I(t)\)をかけるという形になっている。これは、感染人口S(t)が減れば減るほど、感染する人口も減るという現象を表すために行われているのです。

回復率・隔離率γについて、SIRモデルにおける考え方

このSIRモデルでは、回復率・隔離率γを考えのにあたり、感染したのちに隔離した、すなわち、これ以上感染させることのないけど感染している状態と完全に回復して免疫を獲得した人を区別できません。

実際に、計算上、どちらの状態であっても、感染を広めるという点と感染することはないという点では、数理モデルからその人たちを除外できるので、関係はありません。

感染期間の考え方

感染期間は、\(\frac{1}{\gamma}\) で表されます。なぜかというと、除去率・隔離率\(\gamma\)というのは、感染した後、単位時間あたりに回復（厳密にはこれ以上移さない状態）する確率なので、それの逆数を取ると、平均でどれくらいの感染期間（厳密には感染させることが可能な期間）なのかが分かるからです。

SIRモデルから言えることとは？

感染初期は、指数関数的に感染者数が増加する

SIRモデルによると、感染初期は、指数関数的に感染者数で増加します。

「証明」

感染初期\((t_{1})\)においては、感染人口\(I(t_{1})\)、隔離人口\(R(t_{1})\)は限りなく少ないことから、感受性人口\(S(t_{1})\)=全人口Nであると近似して考える。

そうすると、SIRモデルの二つ目の式について、以下が成立する。

$$\frac{dI(t_{1})}{dt} = \beta NI(t_{1}) -\gamma I(t_{1})$$

Nは定数ですので、この式は、線形化方程式と見なすことができ、さらに計算することができる。

\begin{eqnarray}\frac{dI(t_{1})}{dt_{1}} &=& \beta NI(t_{1}) -\gamma I(t_{1})　\\ &=& (\beta N -\gamma) I(t_{1}) \\ \Leftrightarrow \int \frac{1}{I(t_{1})} dI(t_{1}) &=& \int(\beta N -\gamma) dt_{1} \\ \Leftrightarrow \log{I(t_{1})} &=& (\beta N -\gamma)t_{1} + C \\ \Leftrightarrow I(t_{1}) &=& e^{(\beta N-\gamma)t_{1}+C} \\ &=& I(0)e^{(\beta N -\gamma)t_{1}}\end{eqnarray}

\((Cは積分定数、I(0) = e^{C})\)

したがって、以下の式が成立することが分かる。

$$ I(t) = I(0)e^{(\beta N -\gamma)t} $$

この式は、感染人口I(t)が感染初期段階において、指数関数的に増大していることを示していることに他ならない。

「証明終わり」

基本再生産数が1未満であれば、流行しない

基本再生産数が1未満であれば、流行せずに、収束します。

先ほどの式より、

$$ I(t) = I(0)e^{(\beta N -\gamma)t} $$

から、\(\beta N -\gamma>0\) を満たすとき、感染症が流行することが分かります。

そのため、式を変形して、

$$R_0 = \frac{\beta N}{\gamma} > 1$$

と考えることができ、この\(R_0\)のことを基本再生産数と言います。

基本再生産数は、一人が感染中に何人へ移すか、その期待値を表します。

この基本再生産数が、\(R_0 > 1\)のときは、感染が流行して指数関数的に増加したのちに落ち着くような結果が得られ、\(R_0 < 1\)のときは、感染症がそもそも流行しません。

\(\frac{\gamma}{\beta}\)を臨界的な人口密度と言い、上記の式から、

$$\frac{\gamma}{\beta}R_0 = N $$

と変形でき、\(N\)が\(\frac{\gamma}{\beta}\)より小さいならば、\(R_0 < 1\)となり、流行は発生しません。

また、実際に感染症が流行した際は、さらに式変形を行い、

\begin{eqnarray}R_0 &=& \frac{\beta N}{\gamma} \\ \Leftrightarrow R_0\gamma &=&\beta N \\ \Leftrightarrow R_0\gamma -\gamma &=&\beta N - \gamma \\\Leftrightarrow R_0 &=& \frac{(\beta N - \gamma)}{\gamma}\end{eqnarray}

として、基本再生産数を求めることが多いです。

その理由として、分子は感染初期段階のデータから近似することで求められることや、\(\frac{1}{\gamma}\)は感染期間であることから、比較的容易に数値が特定できるからです。

どれくらいの人が感染せずに済むのか？

基本再生産数が高くなるほど、かからない人は指数関数的に減少する

自分がかからない間に流行が収束する可能性は十分に存在します。この根拠についても数学的にSIRモデルを用いると証明することができます。

「証明」

流行が完全に終わった状態\((I(\infty)= 0))\)の最終規模\(z =\frac{R(\infty)}{N}\)すなわち、かかった人の割合について考える。

SIRモデルの三つ目の式より、

$$I(t) =\frac{1}{\gamma}\frac{dR(t)}{dt}$$

SIRモデルの一つ目の式に代入すると、

\begin{eqnarray} \frac{dS(t)}{dt} &=& -\beta S(t)\frac{1}{\gamma}\frac{dR(t)}{dt} \\ \Rightarrow \frac{1}{S(t)} \frac{dS(t)}{dt} &=& -\frac{\beta}{\gamma}\frac{dR(t)}{dt} \\ \Rightarrow \frac{1}{S(t)} dS(t) &=& -\frac{\beta}{\gamma}dR(t) \\ \Rightarrow \int_0^{\infty} \frac{1}{S(t)} dS(t) &=& -\frac{\beta}{\gamma}\int_0^{\infty}dR(t) \\ {\small\log{S(\infty)} - \log{S(0)}} &=& {\small -\frac{\beta}{\gamma}(R(\infty)-R(0))} \end{eqnarray}

このとき、\(S(\infty) = (1-z)N, S(0) \simeq N, \\ R(\infty) = zN, R(0) \simeq 0, R_0 = \frac{\beta N}{\gamma}\)

をそれぞれ代入すると、

\begin{eqnarray}\log{((1-z)N)} -\log{N} &=& -\frac{\beta}{\gamma}zN \\ \Rightarrow 1-z &=& e^{-zR_0}\end{eqnarray}

したがって、かかっていない人の割合\((1-z)\)は、基本再生産数が高いほど指数関数的に減少してしまうことが示せた。

「証明終わり」

この証明から、基本再生産数\(R_0\)が高い、つまり、全人口\(N\)が大きいか、臨界的な人口密度\(\frac{\gamma}{\beta}\)が小さいと流行が大きくなり、かかっていない人の割合は指数関数的に減少するということが分かりました。

最終的にかからない人数の求め方

流行が完全に終わった状態（\(I(\infty)= 0\)の時）について考えます。

途中まで考え方は先ほどと一緒です。

SIRモデルの三つ目の式より、

$$I(t) =\frac{1}{\gamma}\frac{dR(t)}{dt}$$

SIRモデルの一つ目の式に代入すると、

\begin{eqnarray} \frac{dS(t)}{dt} &=& -\beta S(t)\frac{1}{\gamma}\frac{dR(t)}{dt} \\ \Rightarrow \frac{1}{S(t)} \frac{dS(t)}{dt} &=& -\frac{\beta}{\gamma}\frac{dR(t)}{dt} \\ \Rightarrow \frac{1}{S(t)} dS(t) &=& -\frac{\beta}{\gamma}dR(t) \\ \Rightarrow \int_0^{\infty} \frac{1}{S(t)} dS(t) &=& -\frac{\beta}{\gamma}\int_0^{\infty}dR(t) \\ {\small\log{S(\infty)} - \log{S(0)}}&=& {\small -\frac{\beta}{\gamma}(R(\infty)-R(0))} \end{eqnarray}

となります。

ここから、少しだけ式変形の仕方を変えていきます。

\(S(0) \simeq N,R(0) \simeq 0\)より、

\begin{eqnarray} \log{\frac{S(\infty)}{N}} &=& -\frac{\beta}{\gamma}R(\infty) \\ \Rightarrow \frac{S(\infty)}{N} &=& e^{-\frac{\beta}{\gamma}R(\infty)}\end{eqnarray}

\(I(\infty) = 0\)より、

\(S(\infty)+ R(\infty) = N \)であるから、

\begin{eqnarray} S(\infty) &=& N e^{-\frac{\beta}{\gamma}(N - S(\infty))} \end{eqnarray}

よって、最終的にかからない人数を求める式が導き出せました。

したがって、全人口\(N\)と臨界的な人口密度\(\frac{\gamma}{\beta}\)がわかれば求められることが分かりました。

SIRモデルでシミュレーションしてみた

シミュレーションの結果

SIRモデルは離散化することで、シミュレーションが可能です。

実際にプログラミングを行って、シミュレーションをしてみた結果がこちらです。

基本再生産数\(R_0=1.8\)のとき

条件1：\(N = 1000000.0 \\ S(0) = 999990.0 \\ I(0) = 10.0 \\ R(0) = 0.0\\ \gamma = 0.5 \\ \beta^{'} = 0.9 \)

条件1でシミュレーションした結果が、図2のグラフになります。

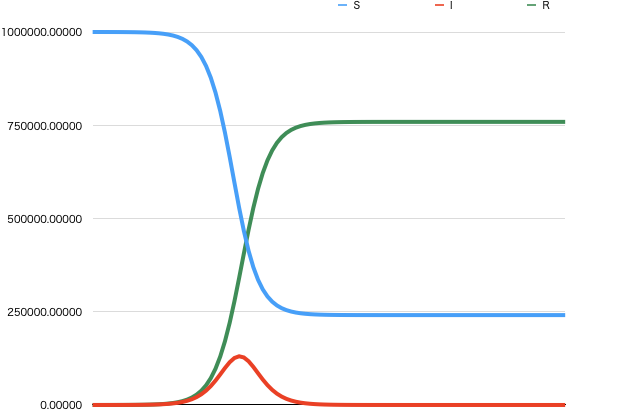
基本再生産数\(R_0 > 1\)であるため、感染人口が指数関数的に増大したのちに、ピークを迎え、収束していることが分かります。

基本再生産数\(R_0=3.0\)のとき

条件2：\(N = 1000000.0 \\ S(0) = 999990.0 \\ I(0) = 10.0 \\ R(0) = 0.0 \\ \gamma = 0.5 \\ \beta^{'} = 1.5\)

条件2でシミュレーションした結果が、図3のグラフになります。

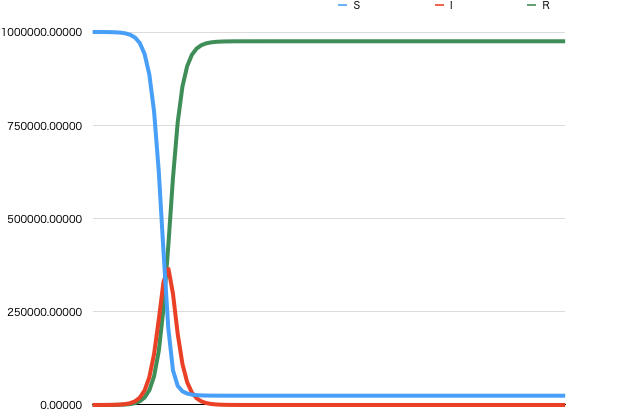
基本再生産数\(R_0 = 1.8\)の場合と比較して、感染人口のピークが高くなっており、かつピークを迎えるのが早くなっています。また、ほとんどの人が最終的に感染してしまいます。

基本再生産数\(R_0=0.98\)のとき

条件3：\(N = 1000000.0 \\ S(0) = 999990.0 \\ I(0) = 10.0 \\ R(0) = 0.0 \\ \gamma = 0.5 \\ \beta^{'} =0.49\)

条件3でシミュレーションした結果が、図4のグラフになります。

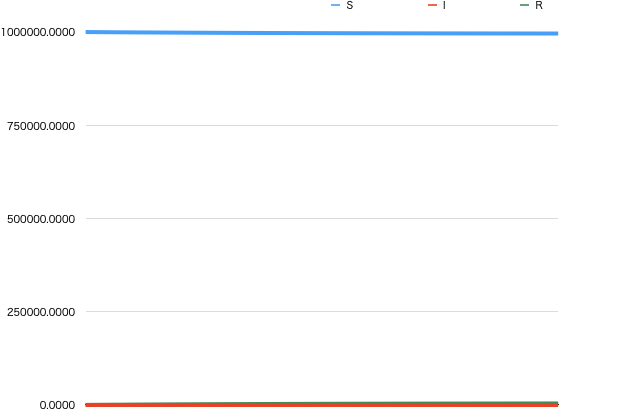
基本再生産数\(R_0 < 1\)であることから、感染は指数関数的に増加することもなく、流行しないということが分かります。

基本再生産数の値が低いほど、流行のピークが小さくかつピークを迎えるまでに時間を要する

基本再生産数の値を感染率を変更することにより変えて、それぞれについて感染人口の変化の仕方を同じグラフにしてまとめました。その結果が、図5のグラフになります。

グラフからも分かる通り、基本再生産数の値が低いほど、流行のピークが小さくかつピークを迎えるまでに時間を要すると言えます。

このことから、感染症の流行を抑えるには、この基本再生産数を低くするということがいかに重要かが分かります。

基本再生産数を低くするには、\(R_0 = \frac{\beta N}{\gamma}\)より、感染率\(\beta^{'}\)を下げることは感染症ごとに依存してしまうため厳しいですが、隔離率\(\gamma\)を上げる、つまり感染に起因する接触を減らせば減らすほど、分母が大きくなるため有効です。

シミュレーションのプログラミングコード

上記のグラフ等を作成するために使用したプログラミングのシミュレーション用のコードになります。言語はSwiftです。

import Cocoa

var N = 1000000.0/*全人口*/
var I_p = 10.0/*感染人口*/,R_p = 0.0/*隔離人口*/
var S_p = N-I_p/*感受性人口*/
var S:Double/*感受性人口*/,I:Double/*感染人口*/,R:Double/*隔離人口*/,R_0:Double/*基本再生産数*/
let gamma = 0.5/*回復率・隔離率(単位時間あたりの回復する確率)*/,beta = 0.9/*感染率(単位時間あたりに何人へ移すか)*/
R_0 = beta/gamma 
for _ in 0...100 {
    S = -(beta*S_p*I_p/N)
    I = beta*S_p*I_p/N - gamma*I_p
    R = gamma*I_p
    S_p = S_p + S
    I_p = I_p + I
    R_p = R_p + R
    print("\(S_p),\(I_p),\(R_p)")
}

SIRモデルについて【まとめ】

SIRモデルの特徴

• 感染初期は、指数関数的に感染者数が増加する
• 基本再生産数が1未満であれば、流行しない
• 基本再生産数が高いほど、かからない人は指数関数的に減少する
• 基本再生産数が低いほど、流行のピークが小さくかつピークを迎えるまでに時間を要する

これまで、SIRモデルについて様々な角度から考察をしてきました。この記事を読んだことで、少しでもSIRモデルについての理解が深まっていれば幸いです。また、SIRモデルは感染症の数理モデルの中では一番簡易的なモデルですので、興味を持った方はぜひ、さらに難易度の高い数理モデルに挑戦してみてください。

参考文献

1. "伝染病流行の数理モデル","稲葉 寿"(2020,4,7アクセス) https://www.ms.u-tokyo.ac.jp/~inaba/inaba2000_kaiyouken.pdf
2. "感染病の数学予測モデルの紹介(SIRモデル）","トーマス セルゲイ"（2020,4,7アクセス）https://qiita.com/kotai2003/items/3078f4095c3e94e5325c
3. "感染症についてSIRモデルから学んだこと","独立行政法人経済産業研究所 関沢 洋一"（2020,4,7アクセス） https://www.rieti.go.jp/jp/columns/a01_0545.html
4. "伝染病（感染症）のモデル","奈良女子大学 情報科学科 大域情報学"（2020,4,7アクセス）http://gi.ics.nara-wu.ac.jp/~takasu/lecture/global/H22-global-8.pdf