SEIRモデルについて、詳しく知りたいと思っている方へ向けた記事になります。
この記事を読むことで、SEIRモデルについての理解とシミュレーションによって、どのように感染症が広まっていくのかが分かるようになります。
実際に、大学で数学を学んだ経験から、分かりやすく解説していきます。
SEIRモデルとは何か、分かりやすく解説します

SEIRモデルの定義
仮定
- 全ての人がS,E,I,Rのいずれかに分類される
- 感染症以外による人口の増減が起こらない
- 一度感染すると、免疫を獲得して、二度とかからない
微分方程式
$$\begin{eqnarray}\frac{dS(t)}{dt} &=& -\beta S(t)I(t) \\ \frac{dE(t)}{dt} &=& \beta S(t)I(t) -\epsilon E(t)\\ \frac{dI(t)}{dt} &=& \epsilon E(t) -\gamma I(t) \\ \frac{dR(t)}{dt} &=& \gamma I(t)\end{eqnarray}$$
\(S(t)\):感受性人口(感染する可能性のある人口)susceptibles
\(E(t)\):潜伏人口(感染して潜伏期間にある人口)exposed ※感染させることはない
\(I(t)\):感染人口(感染している、かつ感染させる能力のある人口) infected/infections
\(R(t)\):隔離人口(病気から回復による免疫保持者、もしくは隔離者・死亡者)recovered/removed
\(\beta\): 伝達係数 \((\beta > 0)\)
\(\beta^{'}\): 感染率 \((\beta^{'} > 0,\beta = \frac{\beta^{'}}{N})\) ※\(N\)は、全人口とする
\(\epsilon\):発症率\((\epsilon > 0)\)
\(\gamma\): 回復率・隔離率 \((\gamma > 0)\)、感染期間 = \(\frac{1}{\gamma})\)
\(t\):時間
SEIRモデルの考え方
SEIRモデルというのは、潜伏期間が発生するような感染症の流行を予測する上で、有効な感染症の数理モデルになります。
基本的な考え方については、こちらの図1にてまとめました。

4つの状態に分けている人口の増減がこのSEIRモデルを用いると、時間変化とともに分かるようになります。
Sは感染する可能性のある人口(実質的に健康でかかったことのない人)、Eは感染しているが、発症していない人口(潜伏期間にあり、感染させる能力はない)Iは感染している人口(厳密には、感染させる能力がある人のみ対象)、Rは隔離されていてこれ以上感染させることのない人や感染症によって死亡した人や免疫を獲得して二度とかからない人を含めます。
SIRモデルとの違い
SIRモデルとの違いとして大きいのは、SEIRモデルの方がより詳細な予測を立てることが可能になるという点です。
その理由として、潜伏期間にある人口についても考慮することができるようになるからです。
実際には、潜伏期間がものすごく長い感染病を予測する際にも用いられており、その際は、人口の感染症以外の原因による増減も考慮し、出生率や死亡率なども考慮したSEIRモデルが使用されるケースもあります。
SEIRモデルの数学的性質については、SIRモデルについて詳しく解説をしているこちらの記事からご覧ください。
-

-
【感染症の数理モデル】SIRモデルとは 分かりやすく説明します【シミュレーションあり】
感染症の数理モデルにおける基本であるSIRモデルについて、理解したいと考えている方へ。 この記事では、SIRモデルについて、どのサイトよりも分かりやすく解説していきます。 SIRモデルの特徴 感染初期 ...
続きを見る
SEIRモデルのシミュレーションをしてみた

シミュレーションの結果
SEIRモデルは離散化することで、シミュレーションが可能です。
実際にプログラミングを行って、シミュレーションをしてみた結果がこちらです。
基本再生産数\(R_0=0.975\)のとき
条件1:\(N = 1000000.0 \\ S(0) = 997000.0 \\ E(0) = 2000.0 \\ I(0) = 1000.0 \\ R(0) = 0.0\\ \gamma = 0.8 \\ \epsilon= 0.5\\ \beta^{'} = 0.78 \)
条件1でシミュレーションした結果が、図2のグラフになります。
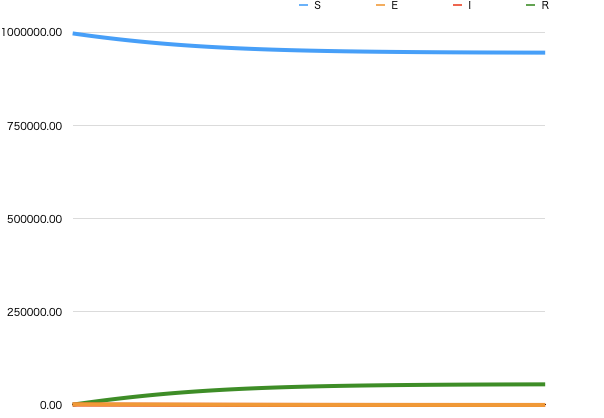
基本再生産数\(R_0 < 1\)であるため、潜伏人口および感染人口の急激な増加が起きない、したがって、流行しないということが分かります。
基本再生産数\(R_0=1.25\)のとき
条件2:\(N = 1000000.0 \\ S(0) = 997000.0 \\ E(0) = 2000.0 \\ I(0) = 1000.0 \\ R(0) = 0.0\\ \gamma = 0.8 \\ \epsilon= 0.5 \\ \beta^{'} = 1.0 \)
条件2でシミュレーションした結果が、図3のグラフになります。
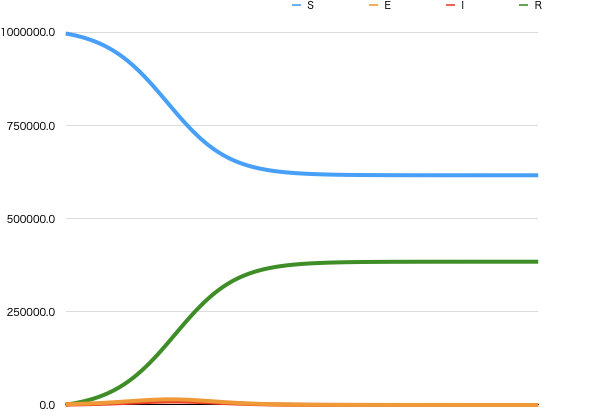
基本再生産数\(R_0 > 1\)であるため、潜伏人口および感染人口の急激な増加が起きたのち、流行が収まっているのが分かります。
基本再生産数\(R_0=2.5\)のとき
条件3:\(N = 1000000.0 \\ S(0) = 997000.0 \\ E(0) = 2000.0 \\ I(0) = 1000.0 \\ R(0) = 0.0\\ \gamma = 0.8 \\ \epsilon= 0.5 \\ \beta^{'} = 2.0 \)
条件3でシミュレーションした結果が、図4のグラフになります。
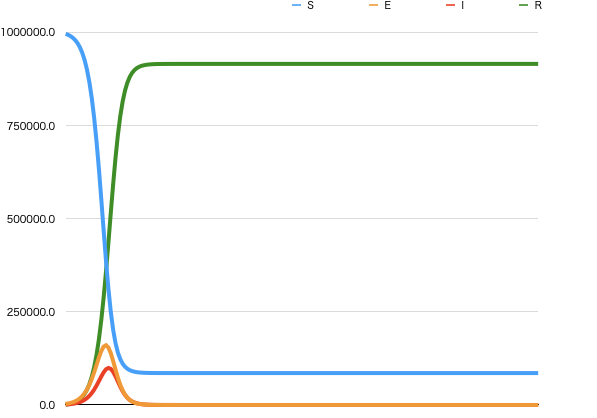
感染者が増加し、流行する過程で、先にピークを迎えるのは潜伏人口であるということが分かります。
また、基本再生産数\(R_0 = 1.25\)のときに比べて、潜伏人口および感染人口の増加の仕方が激しくなっていると言えます。
シミュレーションのプログラミングコード
上記のグラフを作成するために使用したプログラミングのシミュレーション用のコードになります。言語はSwiftです。
import Cocoa
var N = 1000000.0/全人口/,E_p = 2000.0/潜伏人口/,I_p = 1000.0/感染人口/,R_p = 0.0/隔離された人口/
var S:Double/感受性人口/,E:Double/潜伏人口/,I:Double/感染人口/,R:Double/隔離された人口/
var S_p = N - E_p - I_p - R_p/感受性人口/,R_0:Double/基本再生産数/
var gamma = 0.8/隔離率=1/感染期間/, epsilon = 0.5/発症率/
var beta = 2.0/感染率/
R_0 = beta/gamma
for _ in 0..<200{
S = -(betaS_pI_p/N)
E = betaS_pI_p/N - epsilonE_p I = epsilonE_p - gammaI_p R = gammaI_p
S_p = S_p + S
E_p = E_p + E
I_p = I_p + I
R_p = R_p + R
print("(S_p),(E_p),(I_p),(R_p)")
}
【まとめ】SEIRモデルについて
SEIRモデルについて、その特徴や実際に微分方程式を離散化することにより、シミュレーションを行いました。
SEIRモデルは、応用することができる幅が様々あります。その例として、SEIRモデルに出生率や死亡率などを考慮して、何十年スパンの感染症を予測することに活用することもできます。さらには、SEIRモデルよりも精密なシミュレーションをする方法として、MASというのがありますので、気になる方はぜひ調べてみてください。
参考文献
- "【minimize入門】SEIRモデルでデータ解析する♬","ムー ウワン",(2020/4/11 アクセス)https://qiita.com/MuAuan/items/88d5d0c416abb9e9915e
- "感染症流行の予測:感染症数理モデルにおける定量的課題","西浦 博・稲葉 寿",(2020/4/11 アクセス)https://www.ism.ac.jp/editsec/toukei/pdf/54-2-461.pdf
- "感染症流行のシミュレーション","荻田 武史",(2020/4/11 アクセス)http://www.math.twcu.ac.jp/ogita/lec/sim_infection.pdf