どうも、porukaです。
今回は、写像とは何かについて分かりやすく解説していきます!
写像とは、関数を言い換えたものという認識でも大丈夫ですが、証明などで写像を用いる際は注意点があるので、その点も含め、解説していきます。
まず、写像の定義を確認してみましょう。
写像の定義とは
集合AからBへの対応fについて、次の性質を持つとき、特にAからBへの写像とよばれる。
\[Aの\forall a \in Aに対して、\]\[f(a)はBのただ1つの元からなる集合である。\]
<参考>「集合・位相入門」松坂和夫著
これだと難しいかもしれないので、もう少し簡単にすると、
二つの集合が与えられたときに、一方の集合の各元に対し、他方の集合のただひとつの元を指定して結びつける対応のことである。
なるほど、と言った感じでしょうか?
写像というのは、2つの集合が存在して初めて作れるのです。
つまり、写像を作るときには、2つの集合をしっかり定めなければならない、ということです。
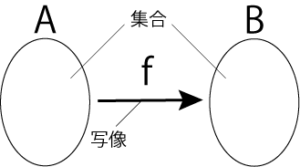
図1. 集合と写像の関係
また、ここで重要なのは、「一方の集合の各元に対し」という部分、それから「ただひとつの元を指定」という部分です。
これがどういう意味かというと、写像というものは、移動する前の元によって構成された集合にある元はすべて移動先が存在し、その移動先は一つに決定するということです。
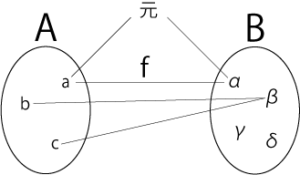
図2.写像である条件
これに対して、写像の定義について確認した時にも出てきましたが、「対応」というものが存在します。「対応」というのは、行先が1つに定まっていないことを許します。つまり、集合Aの各元に対して、集合Bの部分集合が行先となっているということです。
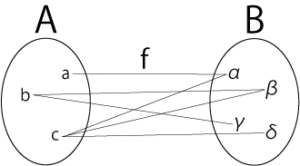
図3.対応に含まれる例
さて、写像と対応の違いを理解できましたでしょうか?
これまでをまとめると、写像というものは以下の条件を満たして成り立ちます。
写像としての必要な条件
- 2つの集合が定義されている。
- 移動前の元によって構成された集合は、その集合に含まれる元の移動先はすべて定まっている。
- 移動した先の元は必ず1つに決定する。
写像を作る際にはこの3点を気を付けましょう!!
また、最初に言ったように写像というものは関数を言い換えたものでもあります。
例えば、
$$f(x)=x^2$$
という関数があるとしたとき、xは定義域であり、f(x)は値域になります。
ここで、上記の2つの規則に従って考えてみましょう。
$$f:\mathbb{R} \rightarrow \{x:x\in\mathbb{R},x>0\}$$
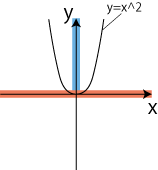
図4.定義域と値域
つまり、移動前の集合というのは、赤色で示したxの定義域であり、移動後の集合は、青色で示したf(x)の値域になるわけです。このことをこれまで、関数と呼んでいましたが、同時に写像でもあるということです。
単射、全射、全単射については、こちらの記事で解説しています!
まとめ
これまで、写像について色々と解説してきましたが、いかがだったでしょうか。
写像を自分で作る際の注意点は...
- 2つの集合が定義されている。
- 移動前の元によって構成された集合は、その集合に含まれる元の移動先はすべて定まっている。
- 移動した先の元は必ず1つに決定する。
この3点をしっかり押さえましょう。