どうも、porukaです。
今回は、数学の中でも難しい、単射、全射、全単射について分かりやすく解説して行きます。
写像とは何かについて復習したい方はこちらへ↓
単射とは
単射の定義は、
$写像f:A \rightarrow B$は、$\forall a,a^{´}\in A$に対し、
$$a \neq a^{´} \Rightarrow f(a) \neq f(a^{´})$$
もしくは、その対偶を取って、
$$f(a) = f(a^{´}) \Rightarrow a = a^{´}$$
が成立すること。
<参考>「集合・位相入門」松坂和夫著
これを見ただけではピンとこないと思うので、もう少しかみ砕いて説明していきます。
Aの元である$a, a^{´}$について、それらが同じものでないとき、写像で行った先も別になるよ、ということを言っているのです。
つまり、Aの元から写像によって移る先にダブり(重複)が存在しない、ということです。
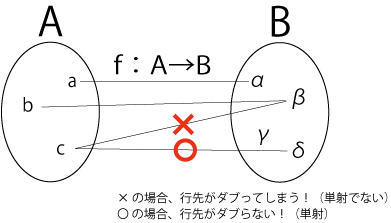
図1.ダブりなし
Aの集合とBの集合それぞれの元の数を考えていましょう。先ほども言ったように、行先にダブりが存在しないということは...
【写像】写像の基本!<大学数学> でも説明した通りに、写像は移動前(今回の場合では集合A)のすべての元に対して定義される、つまり、Aの元はすべてその写像によって移される先が決まっていることから、
単射を満たす場合、Aの元の数の方がBの元の数よりも少ない、ということが分かります。
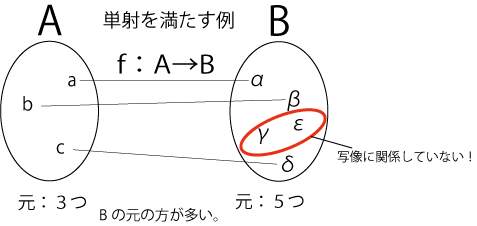
図2.元の数と単射の関係性
これでなんとなく、単射について分かったでしょうか。もし分からない場合は、こちら→ 【写像】写像の基本!<大学数学> から復習をお勧めします!
単射についてばっちり理解してから全射について学習していきましょう!!
全射とは
全射の定義は、
$写像f:A \rightarrow B$があるとき、
$\forall b \in B, \exists a \in A s.t. f(a) = b$
<参考>「集合・位相入門」松坂和夫著
この定義だと正直何を言っているのかさっぱり分からないと思うので、もう少し分かりやすく説明したいと思います。
まず、この定義が言っていることは、Bの元において、その写像を考えたときにあまりとなる元が存在しないということ。
図2の場合を見てもらうと分かる通り、Bにはその写像と関係のない元が残ってしまっています。これが一つもない状況を全射と言います。
AとBの元の数の関係性をそれぞれ考えてみましょう。Bの元で余るものが出てきてしまってはいけないのが全射の条件なので、当然Aの方がBよりも元の数は多くなるはずです。よって、Aの元の方がBの元よりも数が多いのが、前提の条件となります。
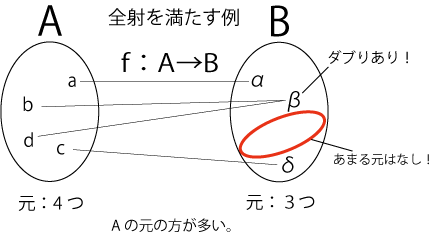
図3.元の数と全射の関係性
補足. この時注意してほしいのは、Aのそれぞれ違う元から行く先が同じであっても良いということです。つまり、単射の条件を満たしていなくても構わないということです。
全単射とは
全単射であるとは、単射と全射の両方を満たす写像であるということ。
ここまで読んで、単射と全射について理解した人であれば、全単射について分かるかと思います。
では実際に、全単射となる例を見てみましょう。
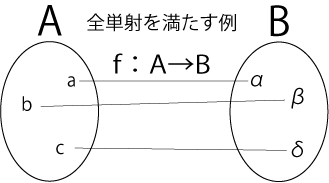
図4.全単射の例
このように、全単射の場合はきれいに行先が決まっているかなり特殊な場合であることが分かるかと思います。
また、集合AとBの元の数は、全単射となる写像が存在する場合は同じになります。
まとめ
単射、全射、全単射というのは、数学を学ぶのみならず、ほかの分野でも幅広く応用される数学の基本でもあるので、しっかりと押さえましょう。以下復習です。
単射
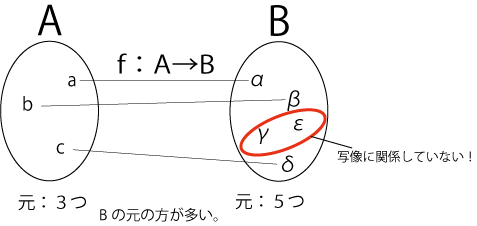
図5.単射の例
全射
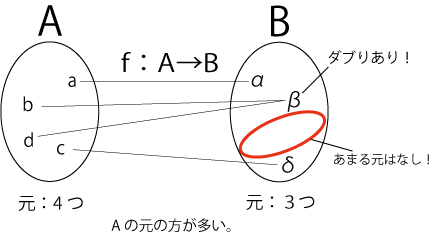
図6.全射の例
全単射
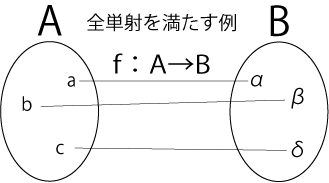
図7.全単射の例
まずは、直観的に各用語を理解していきましょう!単射、全射、全単射と聞いてまず、この図がイメージできるようにしていくことが大切です。